On The Electrodynamics Of Moving Bodies Part:8
§ 7. Theory of Doppler’s Principle and of Aberration
In the system K, very far from the origin of co-ordinates, let there be a source of electrodynamic waves, which in a part of space containing the origin of co-ordinates may be represented to a sufficient degree of approximation by the equations
where
Here (X', Y', Z') and (L0, M0, N0) are the vectors defining the amplitude of the wave-train, and l, m, n the direction-cosines of the wave-normals. We wish to know the constitution of these waves, when they are examined by an observer at rest in the moving system k.
Applying the equations of transformation found in § 6 for electric and magnetic forces, and those found in § 3 for the co-ordinates and the time, we obtain directly
where
From the equation for ω' it follows that if an observer is moving with velocity v relatively to an infinitely distant source of light of frequency ν, in such a way that the connecting line “source-observer” makes the angle φ with the velocity of the observer referred to a system of co-ordinates which is at rest relatively to the source of light, the frequency v' of the light perceived by the observer is given by the equation
This is Doppler’s principle for any velocities whatever. When φ = 0 the equation assumes the perspicuous form
We see that, in contrast with the customary view, when v = −c, ν' = ∞.
If we call the angle between the wave normal (direction of the ray) in the moving system and the connecting line “source observer” φ', the equation for φ'† assumes the form
This equation expresses the law of aberration in its most general form. If φ = 1⁄2π, the equation becomes simply
We still have to find the amplitude of the waves, as it appears in the moving system. If we call the amplitude of the electric or magnetic force A or A' respectively, accordingly as it is measured in the stationary system or in the moving system, we obtain
which equation, if φ = 0, simplifies into
It follows from these results that to an observer approaching a source of light with the velocity c, this source of light must appear of infinite intensity.





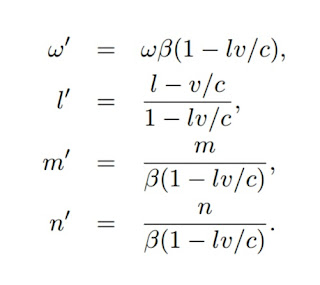













No comments: