On The Electrodynamics Of Moving Bodies Part:7
II. ELECTRODYNAMICAL PART
§ 6. Transformation of the Maxwell-Hertz Equations for Empty Space. On the Nature of the Electromotive Forces Occurring in a Magnetic Field During Motion
Let the Maxwell-Hertz equations for empty space hold good for the stationary system K, so that we have
where (X, Y, Z) denotes the vector of the electric force, and (L, M, N) that of the magnetic force.
If we apply to these equations the transformation developed in § 3, by referring the electromagnetic processes to the system of co-ordinates there introduced, moving with the velocity v, we obtain the equations †
where
Now the principle of relativity requires that if the Maxwell-Hertz equations for empty space hold good in system K, they also hold good in system k; that is to say that the vectors of the electric and the magnetic force—(X', Y', Z' ) and (L', M, N')—of the moving system k, which are defined by their ponderomotive effects on electric or magnetic masses respectively, satisfy the following equations:—
†Editor’s note: In the 1923 English translation, the quantities “ζ” and “ξ” were interchanged in the second equation. They were given correctly in the the original 1905 paper.
Evidently the two systems of equations found for system k must express exactly the same thing, since both systems of equations are equivalent to the Maxwell-Hertz equations for system K. Since, further, the equations of the two systems agree, with the exception of the symbols for the vectors, it follows that the functions occurring in the systems of equations at corresponding places must agree, with the exception of a factor ψ(v), which is common for all functions of the one system of equations, and is independent of ξ, η, ζ and τ but depends upon v. Thus we have the relations
If we now form the reciprocal of this system of equations, firstly by solving the equations just obtained, and secondly by applying the equations to the inverse transformation (from k to K), which is characterized by the velocity −v, it follows, when we consider that the two systems of equations thus obtained must be identical, that ψ(v)ψ(−v) = 1. Further, from reasons of symmetry8 and therefore
and our equations assume the form
As to the interpretation of these equations we make the following remarks: Let a point charge of electricity have the magnitude “one” when measured in the stationary system K, i.e. let it when at rest in the stationary system exert a force of one dyne upon an equal quantity of electricity at a distance of one cm. By the principle of relativity this electric charge is also of the magnitude “one” when measured in the moving system. If this quantity of electricity is at rest relatively to the stationary system, then by definition the vector (X, Y, Z) is equal to the force acting upon it. If the quantity of electricity is at rest relatively to the moving system (at least at the relevant instant), then the force acting upon it, measured in the moving system, is equal to the vector (X', Y', Z'). Consequently the first three equations above allow themselves to be clothed in words in the two following ways:—
1. If a unit electric point charge is in motion in an electromagnetic field, there acts upon it, in addition to the. electric force, an “electromotive force” which, if we neglect the terms multiplied by the second and higher powers of v/c, is equal to the vector-product of the velocity of the charge and the magnetic force, divided by the velocity of light. (Old manner of expression.)
8If, for example, X=Y=Z=L=M=0, and N 6≠ 0, then from reasons of symmetry it is clear that when v changes sign without changing its numerical value, Y' must also change sign without changing its numerical value.
2. If a unit electric point charge is in motion in an electromagnetic field, the force acting upon it is equal to the electric force which is present at the locality of the charge, and which we ascertain by transformation of the field to a system of co-ordinates at rest relatively to the electrical charge. (New manner of expression.)
The analogy holds with “magnetomotive forces.” We see that electromotive force plays in the developed theory merely the part of an auxiliary concept, which owes its introduction to the circumstance that electric and magnetic forces do not exist independently of the state of motion of the system of co-ordinates.
Furthermore it is clear that the asymmetry mentioned in the introduction as arising when we consider the currents produced by the relative motion of a magnet and a conductor, now disappears. Moreover, questions as to the “seat” of electrodynamic electromotive forces (unipolar machines) now have no point.








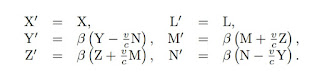







No comments: