On The Electrodynamics Of Moving Bodies Part:4
§ 3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former
Let us in “stationary” space take two systems of co-ordinates, i.e. two systems, each of three rigid material lines, perpendicular to one another, and issuing from a point. Let the axes of X of the two systems coincide, and their axes of Y and Z respectively be parallel. Let each system be provided with a rigid measuring-rod and a number of clocks, and let the two measuring-rods, and likewise all the clocks of the two systems, be in all respects alike.
Now to the origin of one of the two systems (k) let a constant velocity v be imparted in the direction of the increasing x of the other stationary system (K), and let this velocity be communicated to the axes of the co-ordinates, the relevant measuring-rod, and the clocks. To any time of the stationary system K there then will correspond a definite position of the axes of the moving system, and from reasons of symmetry we are entitled to assume that the motion of k may be such that the axes of the moving system are at the time t (this “t” always denotes a time of the stationary system) parallel to the axes of the stationary system.
We now imagine space to be measured from the stationary system K by means of the stationary measuring-rod, and also from the moving system k by means of the measuring-rod moving with it; and that we thus obtain the co-ordinates x, y, z, and ξ, ή, ζ respectively. Further, let the time t of the stationary system be determined for all points thereof at which there are clocks by means of light signals in the manner indicated in § 1; similarly let the time τ of the moving system be determined for all points of the moving system at which there are clocks at rest relatively to that system by applying the method, given in § 1, of light signals between the points at which the latter clocks are located.
To any system of values x, y, z, t, which completely defines the place and time of an event in the stationary system, there belongs a system of values ξ, ή, ζ,τ , determining that event relatively to the system k, and our task is now to find the system of equations connecting these quantities.
In the first place it is clear that the equations must be linear on account of the properties of homogeneity which we attribute to space and time.
If we place x' = x − vt, it is clear that a point at rest in the system k must have a system of values x', y, z, independent of time. We first define τ as a function of x', y, z, and t. To do this we have to express in equations that τ is nothing else than the summary of the data of clocks at rest in system k, which have been synchronized according to the rule given in § 1.
From the origin of system k let a ray be emitted at the time τ0 along the X-axis to x', and at the time τ1 be reflected thence to the origin of the coordinates, arriving there at the time τ2; we then must have ½ (τ0 + τ2) = τ1, or, by inserting the arguments of the function τ and applying the principle of the constancy of the velocity of light in the stationary system:—
Hence, if x' be chosen infinitesimally small,
or
It is to be noted that instead of the origin of the co-ordinates we might have chosen any other point for the point of origin of the ray, and the equation just obtained is therefore valid for all values of x', y, z.
An analogous consideration—applied to the axes of Y and Z—it being borne in mind that light is always propagated along these axes, when viewed from the stationary system, with the velocity 
gives us
Since τ is a linear function, it follows from these equations that
where ais a function φ(v) at present unknown, and where for brevity it is assumed that at the origin of k, τ = 0, when t = 0.
With the help of this result we easily determine the quantities ξ, η, ζ by expressing in equations that light (as required by the principle of the constancy of the velocity of light, in combination with the principle of relativity) is also propagated with velocity c when measured in the moving system. For a ray of light emitted at the time τ = 0 in the direction of the increasing ξ
But the ray moves relatively to the initial point of k, when measured in the stationary system, with the velocity c − v, so that
If we insert this value of t in the equation for ξ, we obtain
In an analogous manner we find, by considering rays moving along the two other axes, that
when
Thus
Substituting for x' its value, we obtain
where
and φ is an as yet unknown function of v. If no assumption whatever be made as to the initial position of the moving system and as to the zero point of τ , an additive constant is to be placed on the right side of each of these equations.
We now have to prove that any ray of light, measured in the moving system, is propagated with the velocity c, if, as we have assumed, this is the case in the stationary system; for we have not as yet furnished the proof that the principle of the constancy of the velocity of light is compatible with the principle of relativity.
At the time t = τ = 0, when the origin of the co-ordinates is common to the two systems, let a spherical wave be emitted therefrom, and be propagated with the velocity c in system K. If (x, y, z) be a point just attained by this wave, then
Transforming this equation with the aid of our equations of transformation we obtain after a simple calculation
In the equations of transformation which have been developed there enters an unknown function φ of v, which we will now determine.
For this purpose we introduce a third system of co-ordinates K', which rel-atively to the system k is in a state of parallel translatory motion parallel to the axis of Ξ,† such that the origin of co-ordinates of system K' moves with velocity −von the axis of Ξ. At the time t = 0 let all three origins coincide, and when t = x = y = z = 0 let the time t' of the system K' be zero. We call the co-ordinates, measured in the system K', x', y', z', and by a twofold application of our equations of transformation we obtain
Since the relations between x', y', z' and x, y, z do not contain the time t, the systems K and K' are at rest with respect to one another, and it is clear that the transformation from K to K' must be the identical transformation. Thus
5The equations of the Lorentz transformation may be more simply deduced directly from the condition that in virtue of those equations the relation x2 + y2 + z2 = c2t2 shall have as its consequence the second relation ξ2 + η2 + ζ2 = c2τ2
†Editor’s note: In Einstein’s original paper, the symbols (Ξ, H, Z) for the co-ordinates of the moving system k were introduced without explicitly defining them. In the 1923 English translation, (X, Y, Z) were used, creating an ambiguity between X co-ordinates in the fixed system K and the parallel axis in moving system k. Here and in subsequent references we use Ξ when referring to the axis of system k along which the system is translating with respect to K. In addition, the reference to system K' later in this sentence was incorrectly given as “k” in the 1923 English translation.
We now inquire into the signification of φ(v). We give our attention to that part of the axis of Y of system k which lies between ξ = 0, η = 0, ζ = 0 and ξ = 0, η= l, ζ = 0. This part of the axis of Y is a rod moving perpendicularly to its axis with velocity v relatively to system K. Its ends possess in K the co-ordinates
and
The length of the rod measured in K is therefore l/φ(v); and this gives us the meaning of the function φ(v). From reasons of symmetry it is now evident that the length of a given rod moving perpendicularly to its axis, measured in the stationary system, must depend only on the velocity and not on the direction and the sense of the motion. The length of the moving rod measured in the stationary system does not change, therefore, if v and −v are interchanged. Hence follows that l/φ(v) = l/φ(-v) , or
It follows from this relation and the one previously found that φ(v) = 1, so that the transformation equations which have been found become
where
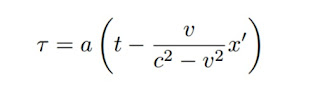
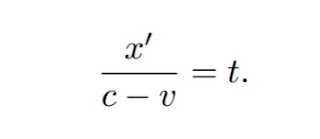
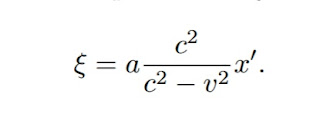
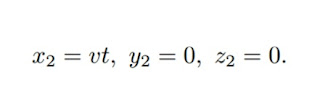
No comments: