On The Electrodynamics Of Moving Bodies part:11
§ 10. Dynamics of the Slowly Accelerated Electron
Let there be in motion in an electromagnetic field an electrically charged particle (in the sequel called an “electron”), for the law of motion of which we assume as follows:—
If the electron is at rest at a given epoch, the motion of the electron ensues in the next instant of time according to the equations
where x, y, z denote the co-ordinates of the electron, and m the mass of the electron, as long as its motion is slow.
Now, secondly, let the velocity of the electron at a given epoch be v. We seek the law of motion of the electron in the immediately ensuing instants of time.
Without affecting the general character of our considerations, we may and will assume that the electron, at the moment when we give it our attention, is at the origin of the co-ordinates, and moves with the velocity v along the axis of X of the system K. It is then clear that at the given moment (t = 0) the electron is at rest relatively to a system of co-ordinates which is in parallel motion with velocity v along the axis of X.
From the above assumption, in combination with the principle of relativity, it is clear that in the immediately ensuing time (for small values of t) the electron, viewed from the system k, moves in accordance with the equations
in which the symbols ξ, η, ζ, X', Y', Z' refer to the system k. If, further, we decide that when t = x = y = z = 0 then τ = ξ = η = ζ = 0, the transformation equations of §§ 3 and 6 hold good, so that we have
With the help of these equations we transform the above equations of motion from system k to system K, and obtain
Taking the ordinary point of view we now inquire as to the “longitudinal” and the “transverse” mass of the moving electron. We write the equations (A) in the form
and remark firstly that εX', εY', εZ' are the components of the ponderomotive force acting upon the electron, and are so indeed as viewed in a system moving at the moment with the electron, with the same velocity as the electron. (This force might be measured, for example, by a spring balance at rest in the last-mentioned system.) Now if we call this force simply “the force acting upon the electron,”9 and maintain the equation—mass × acceleration = force—and if we also decide that the accelerations are to be measured in the stationary system K, we derive from the above equations
With a different definition of force and acceleration we should naturally obtain other values for the masses. This shows us that in comparing different theories of the motion of the electron we must proceed very cautiously.
We remark that these results as to the mass are also valid for ponderable material points, because a ponderable material point can be made into an electron (in our sense of the word) by the addition of an electric charge, no matter how small.
We will now determine the kinetic energy of the electron. If an electron moves from rest at the origin of co-ordinates of the system K along the axis of X under the action of an electrostatic force X, it is clear that the energy withdrawn from the electrostatic field has the value ∫ εX dx. As the electron is to be slowly accelerated, and consequently may not give off any energy in the form of radiation, the energy withdrawn from the electrostatic field must be put down as equal to the energy of motion W of the electron. Bearing in mind that during the whole process of motion which we are considering, the first of the equations (A) applies, we therefore obtain
Thus, when v = c, W becomes infinite. Velocities greater than that of light have—as in our previous results—no possibility of existence.
This expression for the kinetic energy must also, by virtue of the argument stated above, apply to ponderable masses as well.
We will now enumerate the properties of the motion of the electron which result from the system of equations (A), and are accessible to experiment.
1. From the second equation of the system (A) it follows that an electric force Y and a magnetic force N have an equally strong deflective action on an electron moving with the velocity v, when Y = Nv/c. Thus we see that it is possible by our theory to determine the velocity of the electron from the ratio of the magnetic power of deflexion Am to the electric power of deflexion Ae, for any velocity, by applying the law
This relationship may be tested experimentally, since the velocity of the electron can be directly measured, e.g. by means of rapidly oscillating electric and magnetic fields.
2. From the deduction for the kinetic energy of the electron it follows that between the potential difference, P, traversed and the acquired velocity v of the electron there must be the relationship
3. We calculate the radius of curvature of the path of the electron when a magnetic force N is present (as the only deflective force), acting perpendicularly to the velocity of the electron. From the second of the equations (A) we obtain
or
These three relationships are a complete expression for the laws according to which, by the theory here advanced, the electron must move.
In conclusion I wish to say that in working at the problem here dealt with I have had the loyal assistance of my friend and colleague M. Besso, and that I am indebted to him for several valuable suggestions.


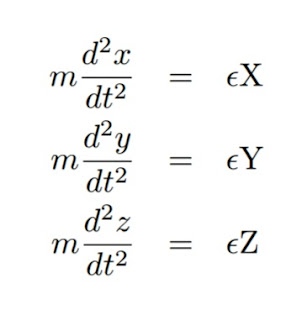


















No comments: